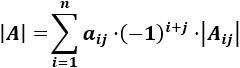ingeniandonos Alqui
sábado, 8 de junio de 2019
viernes, 7 de junio de 2019
miércoles, 5 de junio de 2019
matrices
Cálculo de determinantes de
MATRICES1. Introducción
La función determinante es de gran importancia en el álgebra ya que, por ejemplo, nos permite saber si un matriz es regular (si tiene inversa) y, por tanto, si un sistema de ecuaciones lineales tiene solución. Además, en el caso de que el sistema de ecuaciones tenga una única solución, podemos calcularla aplicando determinantes (regla de Cramer). Otras aplicaciones: el cálculo del producto vectorial de dos vectores y determinar si un conjunto de vectores es linealmente independiente.
Es importante que recordéis:
Denotaremos el elemento de la fila i y la columna j de la matriz A por aij.
Es importante que recordéis:
- Una matriz tiene inversa si su determinante es distinto de 0.
- Las filas de una matriz o sus columnas son linealmente dependientes si, y sólo si, su determinante es 0.
Denotaremos el elemento de la fila i y la columna j de la matriz A por aij.
2. Reglas para cada dimensión
Tenemos una regla para cada dimensión.
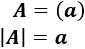
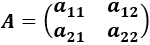 Regla: calculamos el determinante restan el producto de los elementos de las diagonales:
Regla: calculamos el determinante restan el producto de los elementos de las diagonales:
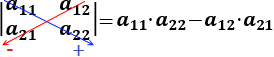
 Regla: calculamos el determinante mediante la llamada regla de Sarrus. Una forma de aplicar la regla de Sarrus es escribir las tres columnas de la matriz seguidas de la primer y la segunda columna:
Regla: calculamos el determinante mediante la llamada regla de Sarrus. Una forma de aplicar la regla de Sarrus es escribir las tres columnas de la matriz seguidas de la primer y la segunda columna:
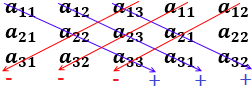 Los elementos de las diagonales con flecha hacia abajo (azul) se multiplican y se suman; los de las otras diagonales (rojo) se multiplican y se restan:
Los elementos de las diagonales con flecha hacia abajo (azul) se multiplican y se suman; los de las otras diagonales (rojo) se multiplican y se restan:
 Normalmente, podemos aplicar la regla de Sarrus sin necesidad de escribir 5 columnas, pero tenéis que pensar vosotros mismos la regla porque es complicado explicarla y entenderla por escrito.
Normalmente, podemos aplicar la regla de Sarrus sin necesidad de escribir 5 columnas, pero tenéis que pensar vosotros mismos la regla porque es complicado explicarla y entenderla por escrito.
Hay dos versiones de la regla: desarrollo por una fila y desarrollo por una columna.
Consejo: desarrollar por la fila o la columna que tenga más ceros.
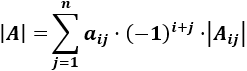 siendo Aij la matriz de dimensión n−1 resultante al eliminar la fila i y la columna j de A.
siendo Aij la matriz de dimensión n−1 resultante al eliminar la fila i y la columna j de A.
Por tanto, si la matriz es dimensión n, tendremos que calcular n determinantes de matrices de dimensión n−1. Esta es la razón por la que solo usamos esta regla cuando no hay otra opción (dimensión mayor que 3).
Para ver la fórmula de forma más intuitiva, observad el desarrollo por la fila 1 de una matriz de dimensión 3:
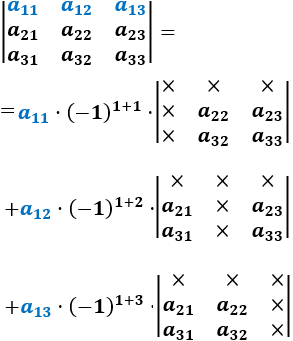 Hemos escrito el símbolo × en las entradas de la matriz que se han eliminado, obteniendo así determinantes de matrices 2x2.
Hemos escrito el símbolo × en las entradas de la matriz que se han eliminado, obteniendo así determinantes de matrices 2x2.
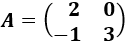 Determinante 2
Determinante 2
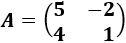

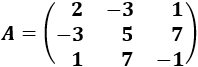
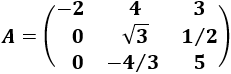
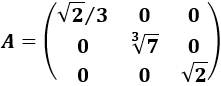
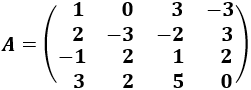 Determinante 9
Determinante 9
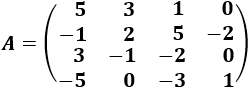
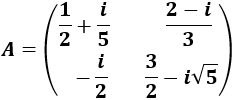
Dimensión 1x1
Si la dimensión de la matriz es 1, sólo tiene un elemento y su determinante es dicho elemento: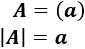
Dimensión 2x2
La matriz cuadrada de dimensión 2 tiene la forma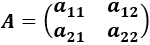
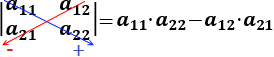
Dimensión 3x3
La matriz cuadrada de dimensión 3 tiene la forma


Ver ejemplo
Regla de Laplace
La regla de Laplace para calcular determinantes se puede aplicar para matrices cuadradas de cualquier dimensión, pero normalmente se hace para dimensión mayor que 3.Hay dos versiones de la regla: desarrollo por una fila y desarrollo por una columna.
Consejo: desarrollar por la fila o la columna que tenga más ceros.
Desarrollo por la fila i de la matriz A de dimensión n:
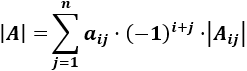
Por tanto, si la matriz es dimensión n, tendremos que calcular n determinantes de matrices de dimensión n−1. Esta es la razón por la que solo usamos esta regla cuando no hay otra opción (dimensión mayor que 3).
Para ver la fórmula de forma más intuitiva, observad el desarrollo por la fila 1 de una matriz de dimensión 3:
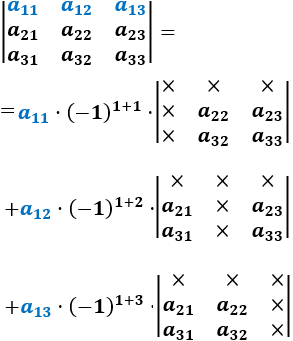
Desarrollo por la columna j de la matriz A de dimensión n es
3. Ejemplos de determinantes
Determinante 1
Matriz de dimensión 2x2
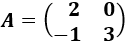 Determinante 2
Determinante 2Matriz de dimensión 2x2
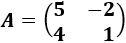
Determinante 3
Matriz de dimensión Determinante 4
Matriz de dimensión 3x3

Determinante 5
Matriz simétrica de dimensión 3x3
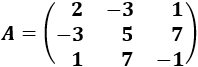
Determinante 6
Matriz de dimensión 3x3 (aplicar Laplace)
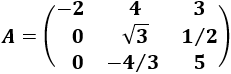
Determinante 7
Matriz diagonal de dimensión 3x3
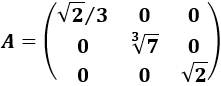
Determinante 8
Matriz de dimensión 4x4
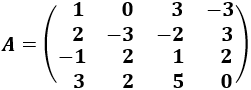 Determinante 9
Determinante 9Matriz de dimensión 4x4
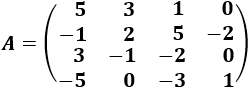
Determinante 10
Matriz de dimensión 3x3 con entradas complejas
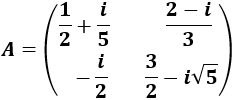
Suscribirse a:
Comentarios (Atom)